آموزش و تمرین دروس دوم راهنمایی

هرکس سه بار بر تو خشمگین شد و درباره ات سخنی ناروا نگفت، او را به دوستی بگیر . [امام صادق علیه السلام]

آموزش و تمرین دروس دوم راهنمایی

رادیکال

در ریاضیات، ریشه دوم یا جذر یک عدد حقیقی غیرمنفی $x$ به صورت $\sqrt x$ نشان داده می‌شود و نتیجه آن عددی حقیقی غیر منفی است که مجذورش (حاصل عددی که در خودش ضرب شود) برابر $x$ است.

برای مثال، جذر عدد 9 برابر 3 است (به صورت 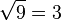$\sqrt 9 = 3$ نمایش می‌یابد) زیرا داریم $3^2 = 3\times3 = 9.$

جذر اغلب در هنگام حل معادله درجه دوم و یا معادله‌های به شکل $a x 2 + b x + c = 0$ استفاده می‌شود، زیرا متغیر $x$ به توان دو رسیده‌است.

طبق قانون بنیادی جبری، دو جواب برای ریشه دوم یک عدد وجود دارد (این دو جواب در ریشه دوم عدد صفر با هم یکی هستند). برای هر عدد حقیقی مثبت دو جواب برای ریشه دوم وجود دارد که این دو جواب عددی هستند که یک بار منفی و یک بار مثبت است (به شکل $\pm\sqrt x$ ).

ریشه دوم اعدادی که مربع کامل نیستند همواره عددی گنگ است، یعنی اعداد را نمی‌توان به صورت کسری از دو عدد صحیح گویا کرد. برای مثال، 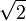$\sqrt 2$ را نمی‌توان دقیقاً به صورت m/n نوشت، که در آن n و m اعدادی صحیح هستند. در هر حال این عدد اندازه قطر مربعی به ضلع یک است. از مدت‌های گذشته، عدد 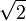$\sqrt 2$ را عددی گنگ می‌دانستند و آن را به فیثاغورث نسبت می‌دادند.

نماد ریشه دوم ( $\sqrt{\ }$ ) برای اولین بار در قرن شانزدهم استفاده شد. به نظر می‌رسد که این علامت از حرف کوچک r برگرفته شده‌است، که بیانگر واژه لاتین radix به معنای ریشه است.

خواص

تابع ریشه دوم، $f(x) = \sqrt{x}$ ، تابعی است از مجموعه اعداد حقیقی غیرمنفی $\mathbb{R}^+ \cup \{0\}$ به خودش.
تابع ریشه دوم $f(x) = \sqrt{x}$ همواره مقداری منحصربه‌فرد برمی گرداند.
برای به دست آوردن هر دو جواب ریشه دوم، ابتدا اولین جواب را به دست آورید و آن را جواب₁ بنامید، سپس آن را از صفر کم کنید تا جواب₂ به دست آید (جواب₂ = 0 ? جواب₁).
خواص زیر، مهم‌ترین خواص ریشه دوم هستند که برای هر عدد حقیقی مثبت $x$ و $y$ صحیح هستند:

$\sqrt{xy} = \sqrt x \sqrt y \qquad \Rightarrow \qquad \sqrt{\left( 100y \right) } \, = \, 10 \cdot \sqrt y$ $\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \qquad \Rightarrow \qquad \sqrt{\frac{x}{100}} = \frac{\sqrt{x}}{10}$ $\sqrt x = x^{1/2}$

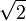ریشه دوم تابعی است از اعداد گویا به اعداد جبری. $\sqrt x$ عددی گویا است، اگر و تنها اگر $x$ عددی گویا باشد که بتوان آن را به صورت کسری از دو عدد مربع کامل نشان داد. به طور کلی، $\sqrt 2$ عددی گنگ است.
در هندسه، تابع ریشه دوم نگاشتی از سطح یک مربع به طول اضلاعش.
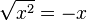بر خلاف عقیده همه، $\sqrt{x^2}$ لزوماً برابر $x$ نیست. این برابری تنها در مواردی که $x$ غیرمنفی باشد صدق می‌کند. اما اگر $x < 0$ باشد، طبق تعریف $\sqrt{x^2}$ است و این یعنی $\sqrt{x^2} = -x$ . در نتیجه برای هر عدد حقیقی $x$ داریم $\sqrt{x^2} = \left|x\right|$ . (قدرمطلق را ببینید)
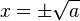فرض کنید $x$ و $a$ اعدادی حقیقی هستند به طوری که math>x^2 = a</math>، و ما می‌خواهیم که $x$ را بیابیم. یکی از اشتباهات رایج این است که آن را به «معادله جذر» تبدیل کنیم و از آن $x = \sqrt a$ را نتیجه بگیریم. این کار نادرست است، زیرا ریشه دوم $x 2$ برابر $x$ نیست، بلکه $\left| x \right|$ است (طبق یکی از خاصیت‌های فوق). اما ما می‌توانیم بگوییم $\left| x \right| = \sqrt a$ ، و در نتیجه $x = \pm\sqrt a$ .
در حسابان، مثلاً وقتی می‌خواهیم اثبات کنیم که تابع ما پیوسته یا مشتق‌پذیر و یا قابل حدگیری است، می‌توانیم از عبارت زیر استفاده کنیم:

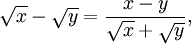
$\sqrt x - \sqrt y = \frac{x-y}{\sqrt x + \sqrt y},$

این عبارت برای تمام $x$ و $y$ های نامنفی به طوری که هر دو صفر نباشند صحیح است.

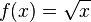نمودار تابع $f(x) = \sqrt x$ به شکل زیر است، این نمودار از نصف یک سهمی ساخته می‌شود:

تابع در تمام $x$ های غیرمنفی پیوسته و برای تمام $x$ های مثبت مشتق‌پذیر است. (در $x = 0$ مشتق‌پذیر نیست، زیرا شیب نمودار یا همان تانژانت در این نقطه ? است) مشتق این تابع برابر است با:

$f$

در سری تیلور $\sqrt{x+1}$ در $x = 0$ می‌توان از بسط نیوتن استفاده کرد:

$\sqrt{x+1}\,\!$	$= 1 + \sum_{n=1}^\infty { (-1)^{n+1} (2n-2)! \over n! (n-1)! 2^{2n-1} }x^n$
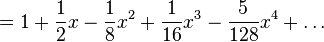	$= 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16} x^3 - \frac{5}{128} x^4 + \dots$
for $\left\| x \right\| < 1$ .

ریشه دوم بیست عدد صحیح مثبت

$\sqrt {1}$	$=\,$	1
$\sqrt {2}$	$\approx$	1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462
$\sqrt {3}$	$\approx$	1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909
$\sqrt {4}$	$=\,$	2
$\sqrt {5}$	$\approx$	2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638
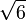$\sqrt {6}$	$\approx$	2.4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457
$\sqrt {7}$	$\approx$	2.6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230
$\sqrt {8}$	$\approx$	2.8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924
$\sqrt {9}$	$=\,$	3
$\sqrt {10}$	$\approx$	3.1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639
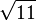$\sqrt {11}$	$\approx$	3.3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609
$\sqrt {12}$	$\approx$	3.4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818
$\sqrt {13}$	$\approx$	3.6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293
$\sqrt {14}$	$\approx$	3.7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307
$\sqrt {15}$	$\approx$	3.8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937
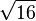$\sqrt {16}$	$=\,$	4
$\sqrt {17}$	$\approx$	4.1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338
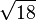$\sqrt {18}$	$\approx$	4.2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386
$\sqrt {19}$	$\approx$	4.3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203
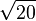$\sqrt {20}$	$\approx$	4.4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276

ساختار هندسی ریشه دوم

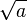ریشه دوم می‌تواند به صورت منحنی ساخته شود. اقلیدس روشی را برای بدست آوردن میانگین هندسی دو عدد مختلف ساخته‌است: Proposition II.14 و Proposition VI.13. میانگین هندسی دو عدد $a$ و $b$ برابر است با $\sqrt{ab}$ و در صورتی که $b = 1$ باشد می‌توان از $\sqrt{a}$ استفاده کرد.

چنین روشی را رنه دکارت هم گفته بود، که می‌توانید آن را در تمرین دوم صفحه دوم ببینید. اگر چه دکارت هیچ ادعایی برای اینکه مطلبی جدید را آورده نداشت و همه افراد آن را از آن اقلیدس می‌دانستند.

سینا ::: دوشنبه 86/12/6::: ساعت 11:13 عصر

نظرات دیگران: نظر

لیست کل یادداشت های این وبلاگ

رادیکال
[عناوین آرشیوشده]

>> بازدیدهای وبلاگ <<

بازدید امروز: 5

بازدید دیروز: 0

کل بازدید :48641

>>اوقات شرعی <<

اوقات شرعی

>> درباره خودم<<

سینا
آموزش و تمرین دروس دوم راهنمایی

>>آرشیو شده ها<<

زمستان 1386

>>اشتراک در خبرنامه<<

>>طراح قالب<<